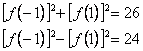34. Megyei Matematikai Verseny, Mezőkövesd 2004.

 

9. osztály

 

 

1./ Mutassuk meg, hogy a  pontosan négy darab 0-ra végződik. Mi az

     utolsó 0-tól különböző számjegy?                                                                    (6 pont)

 

2./ Mennyi az  alakú számok összege, ha  osztható 15-tel?        (6 pont)

 

3./ A valós számok halmazán oldjuk meg grafikusan az    egyenletet,

     ahol az   valós paraméter!                                                                              (9 pont)

 

4./ Egy pozitív  számnak pontosan 12 darab pozitív osztója van. Bizonyítsuk be, hogy

     ezeknek az osztóknak a szorzata  .  Adjuk meg az   legkisebb értékét!    (9 pont)

 

5./ Ábrázoljuk derékszögű koordinátarendszerben azoknak a pontoknak a halmazát, amelyek

     kielégítik az alábbi egyenletet:

                          a./  

                          b./  

                          c./   

                          d./                                                                              (12 pont)

 

6./ Legyen  ,  ahol . Számítsuk ki az  értékét úgy, hogy

     egyszerűsíthető legyen a tört. Végezzük el az egyszerűsítést, majd határozzuk meg az

     x és y összes lehetséges értékét!                                                                       (12 pont)

 

 

 

 

 

 

10. osztály

 

 

 

1.)  Apa, anya és egyetlen gyermekük életkorának összege 100. Apa és anya egykorú, és az

      életkorukat jelző számnak 3-mal több pozitív osztója van, mint a gyermek esetében. Hány

      évesek külön-külön, ha tudjuk, hogy a gyermek már iskolás, de még nem jár egyetemre?

                                                                                                                                    (6 pont)

 

2.)  Legyen az ABC derékszögű háromszög átfogója AB. A B csúcsból induló belső

      szögfelező az AC oldalt D-ben, a háromszög köré írt körét E-ben metszi. Igazoljuk, hogy

      az AE szakasz mértani közepe az ED és az EB szakasznak!                               (6 pont)

 

3.)  Adjuk meg azokat a lineáris   függvényeket, amelyekre egyidejűleg teljesül az alábbi

      két egyenlet:

                    

                                                                                                                                    (9 pont)

4.)  Határozzuk meg az összes olyan pitagoraszi számhármast, amelynek egyik tagja 15.

      (a, b és c pitagoraszi számhármas, ha pozitív egészek és  )            (9 pont)

 

5.)  Oldjuk meg a valós számok halmazán a következő egyenletet:

                                                    (12 pont)

 

6.)  Ha az   egyenletben a valós gyökök köbének különbségét

      elosztjuk a négyzetük különbségével, akkor hányadosul 12-t, maradékul 13-at kapunk.

      Számítsuk ki a p valós paraméter értékét!                                                           (12 pont)

 

 

 

 

 

 

11. osztály

 

 

1.) Egy derékszögű háromszög egyik hegyesszöge 15^o, és az ezzel szemközti befogó 84 cm.

     Számítsuk ki a derékszöget harmadoló egyenesek háromszögön belüli szakaszának pontos

     értékét!                                                                                                               (6 pont)

 

2.) Határozzuk meg az   függvény értelmezési tartományát, érték-

     készletét, és készítsük el a grafikonját!                                                             (6 pont)

 

3.) Oldjuk meg a valós számpárok halmazán a következő egyenletet:

                                                                           (9 pont)

 

4.) Egy háromszög két oldala 6 és 12 egység, a közbezárt szög szögfelezője  . Ez a szög-

     felező két háromszögre bontja az eredeti háromszöget. Számítsuk ki az ezekbe írt körök

     sugarát!                                                                                                              (9 pont)

 

5.) Az ABC háromszög C csúcsánál lévő szög derékszög,  az   vektorok  skaláris

     szorzata 576, a   vektoroké 100.  Számítsuk ki a háromszög oldalait és szögeit! 

                                                                                                                              (12 pont)                                                                                     

 

6.) Az   egyenletben határozzuk meg az   valós paraméter

     értékét úgy, hogy az egyenletnek ne legyen valós gyöke.                              (12 pont)

 

 

 

 

 

 

12. osztály

 

 

1.) Bizonyítsuk be, hogy egy 30 jegyű csupa 4-esből álló, és egy 15 jegyű csupa 8-asból

     álló természetes szám különbsége négyzetszám!                                             (6 pont)

 

2.) Oldjuk meg a valós számok halmazán a következő egyenletet:

                                         (6 pont)

 

3.) Egy kocka élfelező pontjai, valamint a lapközéppontjai is meghatároznak egy-egy,

     síklapokkal határolt testet. Mekkora a két test felszínének aránya, illetve a térfogatok

     aránya?                                                                                                             (9 pont)

 

4.) Oldjuk meg a valós számok halmazán a következő egyenlőtlenséget:

                                                                                                (9 pont)

 

5.) Az   egyenletben határozzuk meg az   valós

     paraméter értékét úgy, hogy az egyenletnek legyen valós megoldása  - re.

                                                                                                                             (12 pont)

 

6.) Egy forgáskúpot elmetszünk két olyan síkkal, amelyek átmennek a kúp csúcspontján.

     A síkok olyan húrokat metszenek ki az alapkörből, amelyek  6, illetve  8 egységre vannak

     a kör középpontjától. A síkmetszetek területei rendre  , illetve  .

     Mekkora a kúp térfogata?                                                                               (12 pont)