
Bezirks-Mathematik-Wettbewerb Nr.35 , Mezőkövesd, 2005.
Klasse 9.
1.) In jedes Feld folgender Zahlenpyramide schreiben wir die Summe der zwei Zahlen, die unter dem genannten Feld stehen. Wie groß ist das Produkt von x und y, wenn beide Zahlen Primzahle sind und eine von den beiden kleiner als 10 ist?
1220
1
x
y
1
(6 Punkte)
2.) Eine vierstellige Zahl, an deren letzten Stelle die 9 steht, ändern wir so, daß wir die 9 von der letzten Stelle löschen, und sie an die erste Stelle schreiben.
Ist es möglich, daß die Differenz der zwei Zahlen 3000, bzw. 3006 ist?
(6 Punkte)
3.) Man beweise, daß folgender Satz bei jeder Primzahl, die größer als 3 ist stimmt:
Das Quadrat dieser Primzahle, dividiert durch 12 gibt immer den Restwert 1 (9 Punkte)
4.) Man löse graphisch folgende Gleichung in der Menge der reellen Zahlen:
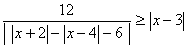
(9 Punkte)
5.) Sei
, wo x und y positive reelle Zahlen sind. Bei welchen Zahlendreiern stimmt folgende Gleichheit?
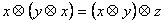
(12 Punkte)
6.) Sei
.
Man rechne die Ausdrücke x+y und xy aus. Wann sind x, y, x+y és xy auszulegen?
(12 Punkte)
Klasse 10.
1.) Man löse folgende Gleichung in der Menge der reellen Tripel:
(6 Punkte)
2.) Man löse folgende Gleichung in der Menge der reellen Zahlen:
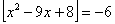
(
ist die größte ganze Zahl kleiner oder gleich x ) (6 Punkte)
3.) An einem Schachturnier haben zwei Klassen – die Klasse 9 und die Klasse 10 – teilgenommen, wo jeder Schüler mit jedem anderen ein Matsch gespielt hat. Die Anzahl der Schüler von der Klasse 9 war 2x so viel, wie die Anzahl der Schüler von der Klasse 10. Die Schüler von der Klasse 10 haben alle ihre Matsche gegenüber denen von der Klasse 9 gewonnen und sie haben 10 Punkte mehr bekommen, als die Schüler von der Klasse 9. Wieviel Schüler gab es in der Klasse 10, und wieviel Punkte haben sie insgesamt erreicht?
(Beim Sieg bekommt man 1 Punkt, beim Unentschieden 0,5 Punkte).
(9 Punkte)
4.) In ein symmetrisches Trapez kann man einen solchen Kreis schreiben, dessen Radius
10 cm ist. Die Mediane des Trapezes ist 20,5 cm. Man berechne den Radius des Kreises, der um das Trapez zu schreiben ist. (9 Punkte)
5.) Der Quotient des Quadratmittels und des geometrischen Mittels von den positiven Zahlen a und b ist:
. Man berechne das Verhältnis von a und b . (12 Punkte)
6.) a.) Bei welcher reellen p Zahl ist die Gleichheit
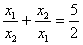
auf die reellen Würzel
und
der Gleichung
wahr?
b.) Gibt es eine solche „p” ganze Zahl, wo die größere Wurzel der Gleichung mit der kleineren dividierbar ist? (12 Punkte)
Klasse 11.
1.) In einem Dreieck teilt eine seiner Höhen die gegenüberliegende Seite in einem Verhältnis von 1:3. Die auf dieser Seite liegenden Winkel sind α und β, wo β=2 α. Wie groß sind die Winkel des Dreiecks?
(6 Punkte)
2.) Man rechne den genauen Wert folgender Summe:
(6 Punkte)
3.) In einem ABC Dreieck sind AB=30, AC=15 és a
Die durch den Halbierungspunkt F ( wo F auf der Seite AB liegt) gezogene FP Gerade schneidet ein solches Dreieck vom ABC Dreieck aus, dessen Flächeninhalt ein Drittel vom Flächeninhalt des ABC Dreieck ist. In welchemVerhältnis steht der Umfang der AFP Dreieck mit dem Umfang des Vierecks BCPF?
(9 Punkte)
4.) Man bestimme den Wert des
reellen Parameters, damit folgender Ausdruck bei keiner reellen Zahl x auszulegen ist:
(9 Punkte)
5.) Man drehe die Punkte
um das Origo
um
in positive Richtung, und dann dehne die Weite zwischen diesen Punkten und dem Origo auf das Doppelte. Die so erhaltenen Punkte sind
Man beweise, daß die Halbierungspunkte der Strecken
ein Parallelogramm bilden.
(12 Punkte)
6.) Man gebe die Menge der reellen Zahlen, wo sich die unten genannten Ungleichungen gleichzeitig erfüllen:
(12 Punkte)
Klasse 12.
1.) In einer arithmetischen Folge ist bei
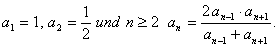
Man rechne das Produkt der ersten fünf Glieder aus.
(6 Punkte)
2.) Das Verhältnis zwischen drittklassiger wiederholter und unwiederholter Kombination von n Elementen ist
Wie groß ist „n”? (6 Punkte)
3.) In einem ABC Dreieck sind
Man drehe das Dreieck um die AB Seite und rechne den genauen Wert des Radius von der maximalen Kugel aus, die in den, auf dieser Weise entstandenen Rotationskörper zu schreiben ist.
(9 Punkte)
4.) Das Volumen eines abgestumpften Kegels ist
seine Oberfläche
Man rechne den Radius des Grund- und Deckkreises, die Höhe und die Erzeugende aus, wenn man weiß, daß der abgestumpfte Kegel eine eingeschriebene Kugel hat.
(9 Punkte)
5.) Drei Geschwister haben insgesamt 10 Mio HUF geerbt. Sie haben ihr Geld in verschiedenen Geldinstituten angelegt. Das Geld von dem ersten Bruder trug 8% Zinsen, das von dem zweiten 2% weniger, als das von dem dritten. Nach einem Jahr hat der erste Bruder 240.000 HUF, der zweite 300.000 HUF, der dritte 480.000 HUF Zinsen bekommen. Was für eine Summe haben sie einzelweise bekommen und wie groß war der Zinsfuß?
(12 Punkte)
6.) In einem Schachtel gibt es n Stk rote und 2x so viel grüne Kugel
, die mit Hand nicht zu unterscheiden sind. Wir ziehen 3 Stk aus dem Schachtel heraus, die wir nicht zurückstecken. Wie groß soll n sein, damit die Wahrscheinlichkeit größer, als 0,25 ist, wenn wir mindestens 2 rote Kugel zwischen den 3 herausgezogenen haben wollen?
(12 Punkte)
Mündliche Aufgaben
Klasse 9.
1.) a.) Man beweise, daß folgender Satz immer stimmt:
Das Quadrat einer ungeraden ganzen Zahl, dividiert durch 8, gibt immer den Restwert 1.
b.) Ist es möglich, daß die Summe der Quadrate von 99 Stk ungeraden Zahlen ist gleich mit dem Quadrat einer ( der 100-sten ) ungeraden Zahl?
2.) Ein Fahrzeug fährt auf der Autobahn in gleichmäßigem Tempo. Auf einem Kilometerstein sieht der Fahrer eine zweistellige Zahl. Eine Stunde später sieht er auf einem nächsten Kilometerstein wieder eine zweistellige Zahl, die die gleichen Ziffer, wie vorher hat, nur in umgekehrter Reihenfolge. Vier Stunden später kommt der Fahrer zu einem solchen Kilometerstein, auf dem wieder die gleichen Ziffer, wie auf dem ersten Kilometerstein sind, nur noch eine 0 steht zwischen diesen beiden.
Mit wieviel km/h Geschwindigkeit fährt das Fahrzeug?
Ersatzaufgabe:
Man bestimme die Werte von x und y so, damit a ∙ b durch 15 teilbar ist, wenn:
a=374x25y und b=422531x.
Klasse 10.
1.) Auf eine gegebenen Strecke AB, die eine Seite eines Dreiecks ist, konstruieren wir das Dreieck ABC. Was ist der geometrische Raum ( Menge ) der „C” Punkte, wenn das Dreieck:
a.) ein rechtwinkeliges b.) spitzwinkeliges c.) stumpfwinkeliges Dreieck ist?
2.) Bei welchen reellen Werten des Parameters „a” hat das Gleichungssystem – bestehend aus den Gleichungen
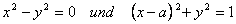
a.) drei b.) vier c.) zwei
Lösungen in der Menge der reellen Zahlenpaare?
Ersatzaufgabe:
a.) Ist es wahr, daß das Spiegelbild des Höhenpunktes – bezogen auf jegliche Seite eines spitzwinkeligen Dreiecks – auf dem der um das Dreieck geschriebene Kreis liegt?
Man beweise diese Behauptung.
b.) Man gebe eine Lösung für das Konstruieren dieses spitzwinkeligen Dreiecks ABC, wenn die Punkte
- (die die Spiegelbilder des Höhenpunktes sind, die sich auf die drei Seiten dieses Dreiecks beziehen) – gegeben sind.
Klasse 11.
1.) Die Seitenlängen eines Dreiecks sind:
Man beweise, daß das Dreieck ein rechtwinkeliges Dreieck ist, dann rechne man die zwei anderen Winkel; den Radius des in das Dreieck schreibbaren, bzw. den Radius des um das Dreieck schreibbaren Kreises aus.
2.) Man bestimme alle mögliche Werte des reellen Parameters „a” so, damit die Gleichung

reelle Lösung hat.
Ersatzaufgabe:
Man schreibe in einen
-igen Kreisausschnitt mit dem Radius r zwei Qudrate. Welches von den beiden hat einen größeren Flächeninhalt und um wielviel Prozent?
Klasse 12.
1.) Sowohl das erste Glied als auch die Differenz einer arithmetischen Folge ist eine Primzahl. Wenn wir die arithmetische Mitte der ersten 10 Glieder mit der arithmetischen Mitte der unter diesen 10 Gliedern befindlichen Elementen von geraden Gliederanzahlen dividieren, ist das Ergebnis:
Wie lautet diese arithmetische Folge?
2.) Man löse folgendes Gleichungssystem in der Menge der reellen Zahlenpaare:
Ersatzaufgabe:
Die harmonische Mitte von drei positiven Zahlen ist
ihre geometrische Mitte ist
und die quadratische Mitte
Wie lautet die arithmetische Mitte?

|
