36. Megyei Matematikai Verseny, Mezőkövesd, 2007.
9. osztály
1.) Oldjuk meg a valós számok halmazán a
egyenletet! (6 pont)
2.) Hány olyan háromjegyű szám van, amelyik sem 2-vel, sem 5-tel nem osztható? (6 pont)
3.) Az ABC hegyesszögű háromszögben az ACB
Igaz-e, hogy a magasságpont és a
C csúcs távolsága egyenlő a háromszög AB oldalával?
(9 pont)
4.) Oldjuk meg a valós számok halmazán az
egyenletet!
(
az a legnagyobb egész szám, amely nem nagyobb az
-nél.) (9 pont)
5.) Az
kifejezésben határozzuk meg az „a” paraméter értékét
úgy, hogy a tört tetszőleges x érték mellett egyszerűsíthető legyen. Végezzük el az
egyszerűsítést, majd határozzuk meg azokat az egész x értékeket, amelyekre az
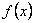
helyettesítési értéke is egész szám! (12 pont)
6.) Oldjuk meg a valós számok halmazán a
egyenlőtlenséget, ahol az „a”
valós paraméter. Milyen „a” érték mellett elégíti ki minden valós szám? Mekkora az „a”,
ha a megoldáshalmaz a
nyílt intervallum? (12 pont)
10. osztály
1.) Egy paralelepipedonnak az egyik csúcsából kiinduló lapátló-vektorai
Fejezzük
ki ezek segítségével az ugyanebből a csúcsból kiinduló
élvektorokat! (6 pont)
2.) Az
egyenletben határozzuk meg az „a” valós paraméter
értékét úgy, hogy az egyenletnek két különböző előjelű valós gyöke legyen! (6 pont)
3.) Oldjuk meg a valós számhármasok halmazán a következő egyenletrendszert:
(9 pont)
4.) Írjunk fel olyan másodfokú egyenletet, amelynek a két valós gyökére érvényes az
egyenlet. Adjuk meg a másodfokú egyenlet gyökeit is!
(9 pont)
5.) Határozzuk meg az
kifejezés értelmezési tartományát, értékkészletét, és hozzuk egyszerűbb alakra! (12 pont)
6.) Egy trapézról tudjuk, hogy van beírt és köré írható köre, és az egyik átló merőleges a
szárra, valamint a terület és a kerület mértékszáma megegyezik. Mekkorák a trapéz
oldalai? (12 pont)
11. osztály
1.) Mennyi a
pontos értéke, ha
(6 pont)
2.) Adjuk meg az
függvény értelmezési tartományát, értékkészletét és
zérushelyeit! (6 pont)
3.) Határozzuk meg az
vektor skaláris szorzatának pontos számértékét, ha
,
, valamint
hajlásszöge
.
(9 pont)
4.) Oldjuk meg a valós számok halmazán a
egyenletet! (9 pont)
5.) Fejtsük meg az alábbi számkeresztrejtvényt:
A
B
C
D
E
F
G
H
K
L
Vízszintes:
A: 18 különböző pont által meghatározott
egyenesek maximális száma
D: 3-as maradéka 2
F:
páratlan és osztható 45-tel. Írd be az
értékét!
G: Az AB szakasz egyik végpontja A
,
felezési pontja
. Írd be a B pont
koordinátáinak szorzatát!
H: A hetvenoldalú konvex sokszög belső szögeinek
összege fokban
L: Az egész számok halmazán értelmezett
kifejezésben az x
lehetséges értékeinek száma.
Függőleges:
A: Az 1186 ötös számrendszerbeli alakja
B: A 40, 96, 104 egység oldalú háromszög köré írt körének sugara
C: A 22 többszöröse
D: Osztható 7-tel
E: A valós gyökök szorzatának abszolút értéke a
egyenletben
K: Tökéletes szám 20 és 30 között. (A tökéletes szám olyan pozitív egész, amely egyenlő
a nála kisebb pozitív osztóinak összegével.) (12 pont)
6.) Az ABC hegyesszögű háromszögben
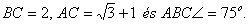
Számítsuk ki a magasságvonalak talppontjai által meghatározott háromszög oldalainak
pontos értékét, és mutassuk meg, hogy ez a talpponti háromszög derékszögű!
(12 pont)
12. osztály
1.) Oldjuk meg a valós számhármasok halmazán a következő egyenletrendszert:
(6 pont)
2.) Az
függvény egyik zérushelye
, és a
szélső értékét az
-nél veszi fel. Mekkora az
Határozzuk meg a függvény
szélső értékét is! (6 pont)
3.) Egy sorozatban
Adjuk meg az
-et az n függvényében,
(zárt alakban) és számítsuk ki az első n elem összegét is! (9 pont)
4.) Az ABCD szabályos tetraéder DC élén jelöljük ki a D-hez közelebbi H harmadoló pontot.
Határozzuk meg az ABH sík és az ABC lap hajlásszögének tangensét! (Pontos értékkel
számoljunk!) (9 pont)
5.) Egy dobozban 12 golyó van, köztük néhány fehér, a többi piros. (A fehérek egyformák,
ugyanígy a pirosak is.) Visszatevés nélkül kihúzunk 3 golyót. Jelöljük
-gyel annak a
valószínűségét, hogy a mintában 1 fehér és 2 piros golyó van. Ha eredetileg kétszer annyi
fehér golyó lett volna a dobozban, és a piros golyók száma ugyanannyi, akkor az 1 fehér és
2 piros golyóból álló minta húzásának valószínűsége
lenne. Hány fehér golyó
volt eredetileg a dobozban?
(12 pont)
6.) Határozzuk meg azoknak a pontoknak a halmazát, amelyekből az
egyenletű körhöz kétszeres hosszúságú érintőket húzhatunk,
mint az
egyenletű körhöz!

|