
35. Megyei Matematikai Verseny, Mezőkövesd, 2005.
9. osztály
1.) Az alábbi számpiramis mezőibe a szóban forgó mező alatti két mezőben szereplő
számok összegét írjuk. Mennyi az x és y szorzata, ha mindkettő prímszám, és
egyikük 10-nél kisebb ?
1220
1
x
y
1
(6 pont)
2.) Egy 9-re végződő négyjegyű számot úgy változtatunk meg, hogy a 9-es számjegyet
a végéről töröljük és az elejére írjuk. Lehet-e a két szám különbsége 3000, ill. 3006?
(6 pont)
3.) Bizonyítsuk be, hogy bármely 3-nál nagyobb prímszám négyzetének a 12-es
maradéka egyenlő 1-gyel! (9 pont)
4.) Oldjuk meg grafikusan a valós számok halmazán a következő egyenlőtlenséget:
(9 pont)
5.) Legyen az
, ahol x és y pozitív valós számok. Milyen számhármasokra
igaz az
egyenlőség? (12 pont)
6.) Legyen
. Számítsuk ki az x+y és xy
kifejezéseket. Mikor értelmezhető x, y, x+y és xy? (12 pont)
10. osztály
1.) Oldjuk meg a valós számhármasok halmazán a következő egyenletet:
(6 pont)
2.) Oldjuk meg a valós számok halmazán az
egyenletet.
(Az
az x egész részét jelenti.) (6 pont)
3.) Egy sakkversenyen 9. és 10. osztályos tanulók vettek részt, ahol mindenki mindenkivel
egy mérkőzést játszott. A 9. osztályosok kétszer annyian voltak, mint a tizedik
osztályosok. A 10. osztályosok minden meccsüket megnyerték a kilencedikesek ellen, így
10-zel több pontot szereztek, mint a kilencedikesek. Hányan voltak a 10. osztályosok, és
hány pontot szereztek összesen? (Egy győzelemért 1 pontot, döntetlenért 0,5-0,5 pontot
kapnak a versenyzők.)
(9 pont)
4.) Egy szimmetrikus trapézba kör írható, amelynek sugara 10 cm. A trapéz középvonala
20,5 cm. Számítsuk ki a trapéz köré írható körnek a sugarát! (9 pont)
5.) Az a és b pozitív számok négyzetes közepének, és mértani közepének hányadosa
. Számítsuk ki az a és b arányát! (12 pont)
6.) a.) Az
egyenlet
és
valós gyökeire az
egyenlőség milyen valós p esetén igaz?
b.) Van-e olyan egész p érték, amelyre az egyenlet nagyobbik gyöke osztható a
kisebbik gyökkel? (12 pont)
11. osztály
1.) Egy háromszögben az egyik magasság a szemközti oldalt 1:3 arányban osztja. Az ezen
az oldalon fekvő egyik szög kétszerese a másiknak. Mekkorák a háromszög szögei?
(6 pont)
2.) Számítsuk ki a következő összeg pontos értékét:
(6 pont)
3.) Az ABC háromszögben AB=30, AC=15 és a
Az AB oldal F felezési
pontján át húzott FP egyenes olyan háromszöget vág le az ABC háromszögből, amelynek
területe egyenlő az ABC háromszög területének egyharmadával. Mekkora az AFP
háromszög és a BCPF négyszög kerületének aránya? (9 pont)
4.) Határozzuk meg az
valós paraméter értékét úgy, hogy a következő kifejezés egyetlen
x valós számra se legyen értelmezhető:
(9 pont)
5.) Az
pontokat forgassuk el az origó körül
-kal pozitív irányba, majd az így kapott pontok origótól mért távolságát nyújtsuk
kétszeresére. A kapott pontok legyenek rendre
Igazoljuk, hogy az
szakaszok felezési pontjai paralelogrammát határoznak meg.
(12 pont)
6.) Adjuk meg azoknak a valós számoknak a halmazát, amelyekre az alábbi két
egyenlőtlenség egyszerre teljesül:
(12 pont)
12. osztály
1.) Egy számtani sorozatban
Számítsuk ki
az első öt tag szorzatát. (6 pont)
2.) n elem harmadosztályú ismétléses és ismétlés nélküli kombinációinak aránya
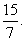
Mekkora az n? (6 pont)
3.) Az ABC háromszögben
Forgassuk meg a
háromszöget az AB oldal körül, majd számítsuk ki a keletkezett forgástestbe írható
maximális nagyságú gömb sugarának pontos értékét! (9 pont)
4.) Egy csonka kúp térfogata
felszíne
Számítsuk ki az alap- és a fedőkör
sugarát, a magasságát és az alkotóját, ha tudjuk, hogy a csonka kúpnak van beírt gömbje.
(9 pont)
5.) Három testvér összesen 10.000.000 Ft-ot örökölt. Pénzüket különböző pénzintézetekben
helyezték el, az első 8%-os kamatra, a második 2%-kal kisebb kamatra, mint a harmadik.
Egy év letelte után rendre 240.000; 300.000; illetve 480.000 Ft kamatot kaptak. Milyen
összeget örököltek külön-külön, és mennyi volt a kamatláb? (12 pont)
6.) Egy dobozban n darab kütyü, és kétszer annyi ketyere van,
amelyek tapintással
nem különböztethetők meg. Visszatevés nélkül kihúzunk 3 darabot. Milyen n esetén lesz
0,25-nál nagyobb annak a valószínűsége, hogy legalább 2 kütyü van a mintában?
(12 pont)
Szóbeli feladatok 2005.
9. osztály
1.) a.) Bizonyítsuk be, hogy egy páratlan egész szám négyzetének 8-as maradéka 1.
b.) Egyenlő lehet-e 99 darab páratlan egész szám négyzetének összege egy újabb
páratlan egész szám négyzetével?
2.) Egy jármű vezetője egy egyenes országúton egyenletes sebességgel haladva egy
kilométerkövön egy kétjegyű számot lát, egy órával később egy újabb kilométerkövön
ugyanazokat a számjegyeket látja, csak fordított sorrendben. Majd négy óra múlva olyan
kilométerkőhöz érkezik, amelyen ugyanaz a két számjegy található, mint az elsőn, csak
közöttük egy 0-val. Mekkora lehet a jármű sebessége?
Tartalék feladat:
Határozzuk meg x és y értékét úgy, hogy az
osztható legyen 15-tel, ha
a=374x25y és b=422531x.
10. osztály
1.) Adott AB szakaszra, mint egyik oldalra megszerkesztjük az ABC háromszöget. Mi a
C pontok mértani helye (halmaza), ha a háromszög
a.) derékszögű b.) hegyesszögű c.) tompaszögű?
2.) Az
egyenletekből álló egyenletrendszernek az „a”
paraméter mely valós értékeinél van
a.) három b.) négy c.) kettő
megoldása a valós számpárok halmazán?
Tartalék feladat:
a.) Igaz-e, hogy egy hegyesszögű háromszögben a magasságpontnak bármelyik oldalra
vonatkozó tükörképe rajta van a háromszög köré írt körön? Állításunkat igazoljuk!
b.) Adjunk eljárást az ABC hegyesszögű háromszög szerkesztésére, ha adott a
magasságpontjának mindhárom oldalra vonatkozó tükörképe, az
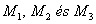
pont.
11. osztály
1.) Egy háromszög oldalainak hossza
Mutassuk meg, hogy a
háromszög derékszögű, majd számítsuk ki másik két szögét, beírható, illetve köré írható
körének sugarát.
2.) Határozzuk meg az „a” valós paraméter összes lehetséges értékét úgy, hogy az

egyenletnek legyen valós megoldása.
Tartalék feladat:
Egy r sugarú
-os körcikkbe írjunk kétféleképpen négyzetet. Melyiknek nagyobb a területe, és hány százalékkal?
12. osztály
1.) Egy számtani sorozat első tagja és differenciája is prímszám. Ha az első 10 tag számtani
közepét elosztjuk a közöttük lévő páros sorszámú elemek számtani közepével, akkor
lesz az eredmény. Melyik ez a számtani sorozat?
2.) Oldjuk meg a valós számpárok halmazán a következő egyenletrendszert:
Tartalék feladat:
Három pozitív szám harmonikus közepe
mértani közepe
négyzetes közepe
Mivel egyenlő a számtani közepük?

|
